Toutes les versions de cet article : [English] [Español] [français]
Para testear este artículo, debemos tener instalado MathGraph32 versión 7.0.0 o posterior.
MathGraph32 versión 7.0 ya nos permite crear una recta de regresión lineal con la herramienta  : simplemente hacemos clic en los puntos y luego en el botón rojo STOP para obtener la recta de regresión lineal de y respecto a x.
: simplemente hacemos clic en los puntos y luego en el botón rojo STOP para obtener la recta de regresión lineal de y respecto a x.
Pero tener una construcción para obtener esta recta de regresión a partir de una matriz puede ser utilizada, por ejemplo, para usarla en regresiones no lineales.
Además, será un excelente ejemplo de aprendizaje sobre MathGraph32, macro construcciones y matrices.
Si simplemente deseamos utilizar las dos macro construcciones (regresión lineal y exponencial), podemos descargarlas al final de este artículo.
Ambas funcionan de la misma manera : están provistas de una matriz de dos columnas (la primera contiene las abscisas de los puntos y la segunda las ordenadas) y la macro proporciona los elementos necesarios para la representación gráfica de la función de correlación.
Creamos una nueva figura en blanco, por ejemplo munida con un referencial.
Vamos a crear una matriz de coordenadas muy sencilla, que nos permitirá, si es necesario, comprobar que no tenemos errores en nuestras fórmulas.
Usamos el ícono  ubicado a la derecha de la barra de herramientas de cálculo y elegimos el elemento Matriz.
ubicado a la derecha de la barra de herramientas de cálculo y elegimos el elemento Matriz.
Rellenamos el cuadro de diálogo como se muestra a continuación.
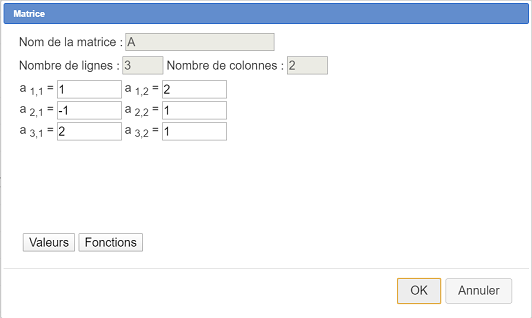
La primera columna contiene las abscisas de los puntos y la segunda las ordenadas.
En nuestros cálculos, no debemos usar 3 como el número de filas de la matriz A porque esta matriz será reemplazada por otra cuando se deba implementar la macro construcción.
Con la herramienta  creamos el siguiente cálculo real :
creamos el siguiente cálculo real :
| Nombre del cálculo | Fórmula | Comentario |
| N | nbrow(A) | En un cálculo real, este es el único tipo de fórmula permitido para obtener el número de filas en una matriz. Por ejemplo, 2*nbrow(A) o nbrow(A+1) serían los cálculos reales denegados. |
En los siguientes cálculos usaremos la función de suma que funciona de la siguiente manera :
suma (fórmula a sumar, nombre variable sumatoria, índice de inicio, índice final, paso)
Los últimos tres parámetros deben ser números enteros con un índice inicial menor o igual que el índice final y el valor del paso debe ser un número entero mayor o igual a 1 (valor 1 el más frecuente).
Así que creamos los siguientes cálculos reales :
| Nombre del cálculo | Fórmula | Comentario |
| mx | suma(A(k,1),k,1,N,1)/N | Contendrá el promedio de las abscisas $\overline{x}$. Por lo tanto, usamos los términos de la primera columna de A. |
| my | suma(A(k,2),k,1,N,1)/N | Contendrá el promedio de las ordenadas $\overline{y}$. Por lo tanto, usamos los términos de la segunda columna de A. |
| vx | suma(A(k,1)^2,k,1,N,1)/N-mx^2 | Contendrá la varianza de x dada por la fórmula $\overline{x^ 2}-(\overline{x})^2$ |
| vy | suma(A(k,2)^2,k,1,N,1)/N-my^2 | Contendrá la varianza de y dada por la fórmula $\overline{y^ 2}-(\overline{y})^2$ |
| covxy | sum(A(k,1)*A(k,2),k,1,N,1)/N-mx*my | Contendrá la covarianza definida por la fórmula $\overline{xy }-\overline{x}\times\overline{y}$ |
| coefcor | covxy/(sqrt(vx)*sqrt(vy)) | Contendrá el coeficiente de correlación lineal, entre 0 y 1. Cuanto más cerca esté de 1, mejor será la correlación. |
| areg | covxy/vx | Coeficiente director de la recta de correlación lineal |
| breg | my-areg*mx | La ordenada en el origen de la recta de regresión que pasa por el punto de coordenadas $(\overline{x},\overline{y})$ |
En esta etapa, podemos guardar la figura que está lista para crear nuestra macro construcción.
En la barra de herramientas superior, haga clic en el icono ![]() que abre las herramientas suplementarias.
que abre las herramientas suplementarias.
El icono  se utiliza para crear la construcción.
se utiliza para crear la construcción.
Hacemos clic una primera vez sobre este icono y elegimos el elemento Elección de objetos fuente numéricos.
Se abre un cuadro de diálogo. Utilizamos el botón Insertar para elegir la matriz A como el único objeto fuente numérico, como se muestra a continuación, luego validamos.
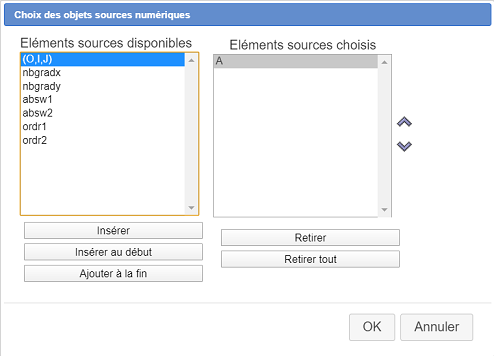
Nuestra macro construcción solo proporcionará objetos finales de tipo numérico.
Hacemos clic nuevamente en el ícono  y elegimos el ítem Elección de objetos finales numéricos.
y elegimos el ítem Elección de objetos finales numéricos.
Seleccionamos los objetos finales numéricos como se muestra a continuación (también podemos incluir la covarianza aquí si lo deseamos) :
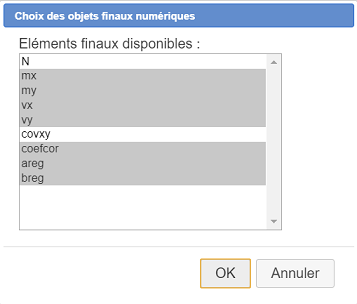
Hacemos clic de nuevo en el icono  y elegimos el ítem Finalizar la construcción en curso.
y elegimos el ítem Finalizar la construcción en curso.
Rellenamos el cuadro de diálogo de la siguiente manera :
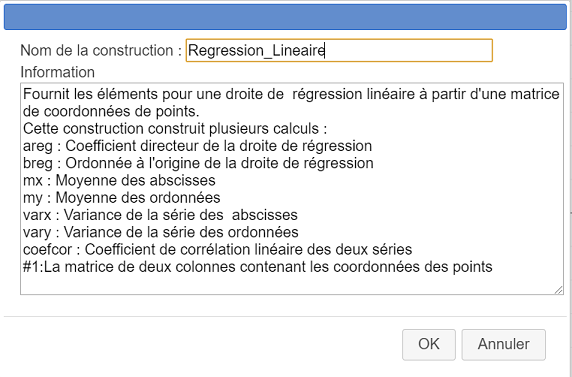
Aquí está el código para ingresar en el campo Información :
Proporciona los elementos para una recta de regresión lineal a partir de una matriz de coordenadas de puntos.
Esta construcción genera varios cálculos:
areg: Coeficiente director de la recta de regresión
breg: Ordenada en el origen de la recta de regresión
mx: Media de las abscisas
my: Media de las ordenadas
varx: Varianza de la serie de abscisas
varía: varianza de la serie de ordenadas
coefcor: coeficiente de correlación lineal de las dos series
#1: La matriz de dos columnas que contiene las coordenadas de los puntosSe utiliza para proporcionar información a los usuarios de nuestra macro construcción.
La última línea que comienza con #1 : proporciona lo que se mostrará como una indicación cuando el usuario elija el primer (y último) objeto fuente de la construcción.
Vamos a guardar nuestra macro construcción en un archivo separado para que podamos usarla en otras figuras.
Utilicemos el icono  (gestión de construcciones) y elegimos el ítem Guardar una construcción de la figura.
(gestión de construcciones) y elegimos el ítem Guardar una construcción de la figura.
Se abre un cuadro de diálogo. La única construcción ya está seleccionada. Hacemos clic en el botón Guardar y guardamos la construcción en la carpeta de nuestra elección con el nombre Regresión_Lineal.mgc, por ejemplo.
Guardemos también nuestra figura con el nombre a nuestra elección (la macro construcción es una de ellas).
Ahora probaremos cómo funciona nuestra construcción en una nueva figura.
Con el ícono  , creamos una figura con un referencial ortonormal.
, creamos una figura con un referencial ortonormal.
Utilicemos el icono  (punto libre) para crear 6 puntos libres (podemos crear más si lo deseamos).
(punto libre) para crear 6 puntos libres (podemos crear más si lo deseamos).
Despleguemos la barra de herramientas de cálculos, hagamos clic en el icono  y elegimos Matriz de coordenadas.
y elegimos Matriz de coordenadas.
Aceptamos el nombre proporcionado por defecto (mat) y luego hacemos clic en los 6 puntos. Finalmente, hacemos clic en el botón rojo DETENER en la parte inferior derecha de la ventana.
MathGraph32 tiene para nosotros :
Ahora incorporaremos nuestra construcción en esta figura y le aplicaremos a esta matriz.
Utilicemos el icono  (gestionar las construcciones) y seleccionemos el elemento Incorporar una construcción desde un archivo.
(gestionar las construcciones) y seleccionemos el elemento Incorporar una construcción desde un archivo.
Vayamos a la carpeta donde guardamos nuestro archivo Regresión_Lineal.mgc, lo seleccionamos y hacemos clic en el botón Abrir. La construcción ahora es parte de tu figura.
Nuevamente usemos el ícono  (gestionar las construcciones) y elegimos el ítem Implementar una construcción de la figura.
(gestionar las construcciones) y elegimos el ítem Implementar una construcción de la figura.
Nuestra construcción única ya está seleccionada. Hacemos clic en el botón Implementar.
Se abre un cuadro de diálogo que nos pide que elijamos nuestro objeto origen (matriz). Le asignamos la matriz mat como se muestra a continuación y validamos :
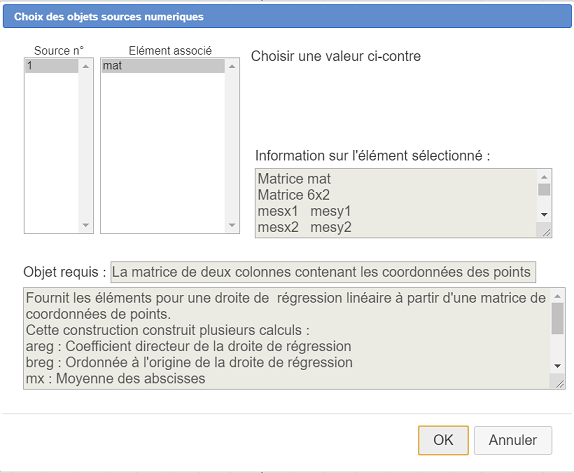
En la barra de herramientas de arriba, usemos el ícono  para ver los objetos numéricos de la figura.
para ver los objetos numéricos de la figura.
En la parte inferior de la lista, veremos los objetos que han sido creados por la construcción, en particular, areg y breg.
Activamos el color rojo, un grosor de trazo de 2 píxeles y activamos la herramienta  que nos permite crear una recta dando una ecuación de la recta en un referencial.
que nos permite crear una recta dando una ecuación de la recta en un referencial.
Como fórmula para la ecuación de la recta, ingresamos : y=areg*x+breg y validamos de la siguiente manera :
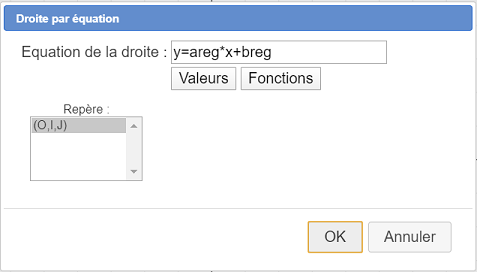
Aparece nuestra recta de regresión. Cuanto más alineados estén los puntos, más cerca estará la recta de ellos.
Ahora crearemos una nueva figura que nos permitirá crear una macro construcción de regresión exponencial.
Utilizamos el icono  para crear una nueva figura.
para crear una nueva figura.
Usamos el ícono  ubicado a la derecha de la barra de herramientas de cálculo y elegimos el ítem Matrix.
ubicado a la derecha de la barra de herramientas de cálculo y elegimos el ítem Matrix.
Creamos la matriz llamada mat como se muestra a continuación :
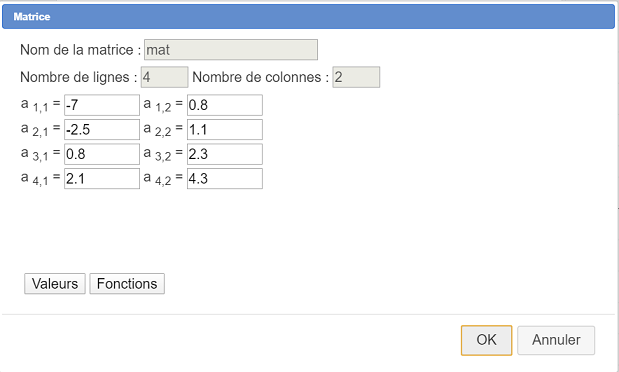
Luego usamos el ícono  para crear un cálculo llamado N con la fórmula nbrow(mat).
para crear un cálculo llamado N con la fórmula nbrow(mat).
Primero recordemos el principio : si la nube parece estar cerca de una curva exponencial, en lugar de acercarnos a ella por regresión lineal (por lo tanto por una recta) intentaremos acercarnos a ella por una curva cuya ecuación es $y=A\times x^{ r}$ (asumimos que las ordenadas de los puntos son todas positivas).
Para $y=Ar^x$⇔$\ln (y)=\ln (A)+ \ln (x^r)$⇔$\ln (y)=\ln (A)+ x\ln (r) $.
Poniendo $y’=\ln{y}, \ln(A)=a$ et $\ln(r)=b$ la última igualdad es por lo tanto de la forma $y’=ax+b$.
La idea es por tanto construir una matriz con dos columnas cuya primera columna sea la misma que la de la matriz mat y la segunda formada por los logaritmos neperianos de los números de la segunda columna de mat.
Aplicaremos a esta matriz nuestra macro construcción de regresión lineal la cual nos proporcionará los valores de areg y breg.
Deduciremos los valores de $A=e^{areg}$ y $r=e^{breg}$
Así que construyamos nuestra nueva matriz.
Utilicemos el icono  ubicado a la derecha de la barra de herramientas de cálculo y elegimos el elemento Matriz por fórmula.
ubicado a la derecha de la barra de herramientas de cálculo y elegimos el elemento Matriz por fórmula.
Rellenamos el cuadro de diálogo como se muestra a continuación.
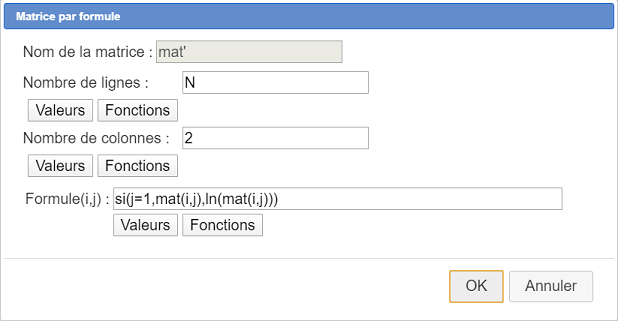
Aquí está la fórmula utilizada :
si(j=1,mat(i,j),ln(mat(i,j)))Utilicemos el icono  (Gestionar las construcciones) y seleccionemos el elemento Incorporar una construcción desde un archivo.
(Gestionar las construcciones) y seleccionemos el elemento Incorporar una construcción desde un archivo.
Vayamos a la carpeta donde guardamos nuestro archivo Regresión_Lineal.mgc, lo seleccionamos y hacemos clic en el botón Abrir.
Nuevamente usamos el ícono  (Gestionar las construcciones) y elegimos el ítem Implementar una construcción de la figura.
(Gestionar las construcciones) y elegimos el ítem Implementar una construcción de la figura.
Nuestra construcción única ya está seleccionada. Hacemos clic en el botón Implementar.
Rellenamos el cuadro de diálogo de la siguiente manera :
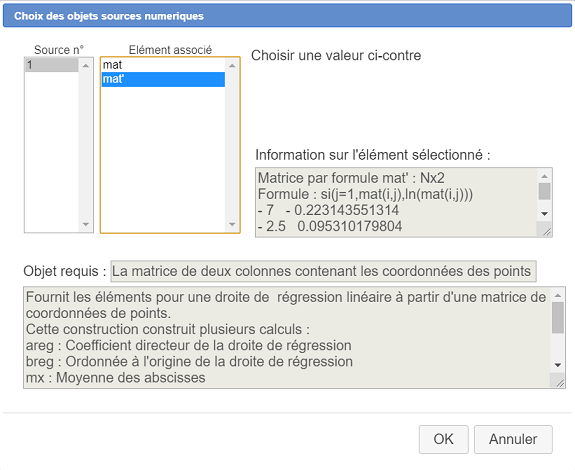
Usando el ícono  ahora podemos ver los objetos creados por la construcción de la macro, incluidos los cálculos areg y breg.
ahora podemos ver los objetos creados por la construcción de la macro, incluidos los cálculos areg y breg.
Ahora usamos el ícono  para crear los siguientes cálculos
para crear los siguientes cálculos
| Nombre del cálculo | Fórmula |
| A | exp(areg) |
| r | exp(breg) |
Ahora creamos la función que proporcionará la fórmula de aproximación de y en x con el ícono < como se muestra a continuación (no marquemos la casilla Trazar la curva )
como se muestra a continuación (no marquemos la casilla Trazar la curva )
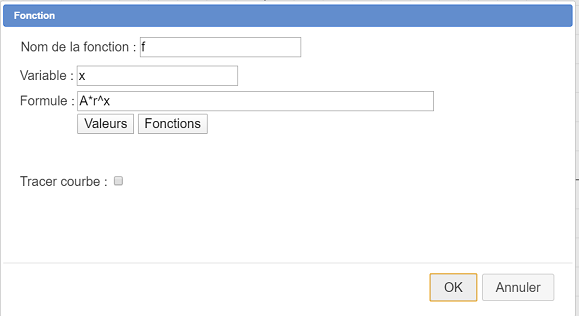
| Nombre de la función | Fórmula |
| f | A*r^x |
Nuestra figura ahora está lista para crear nuestra nueva macro construcción de regresión exponencial.
Activamos la herramienta  de creación de construcciones y elegimos el ítem Elección de objetos fuente numéricos.
de creación de construcciones y elegimos el ítem Elección de objetos fuente numéricos.
Como único elemento fuente elegimos la matriz mat como se muestra a continuación :
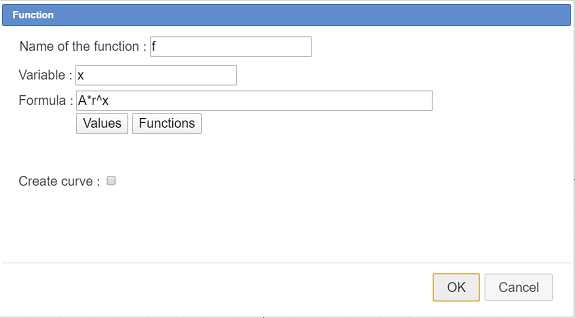
Activemos la herramienta  nuevamente y elijamos el ítem Elección de objetos finales numéricos.
nuevamente y elijamos el ítem Elección de objetos finales numéricos.
Seleccionemos como se muestra a continuación coefcor (coeficiente de correlación), A, r y f :
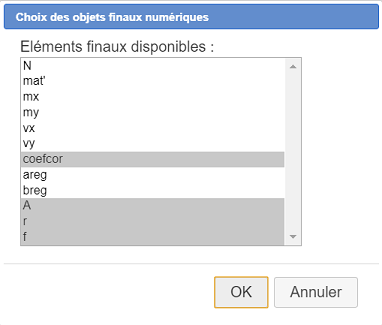
Activemos la herramienta  nuevamente y elijamos el ítem Finalizar la construcción en curso.
nuevamente y elijamos el ítem Finalizar la construcción en curso.
Rellenemos el cuadro de diálogo de la siguiente manera :
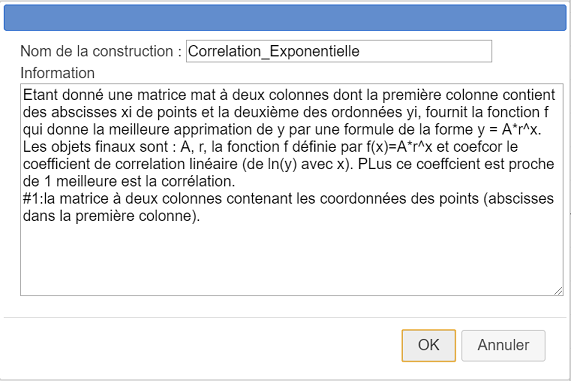
Este es el contenido del campo Información :
Dada una matriz mat de dos columnas cuya primera columna contiene abscisas xi de los puntos y la segunda columna las ordenadas yi, proporciona la función f que dé la mejor aproximación de y mediante una fórmula de la forma y = A*r^x.
Los objetos finales son : A, r, la función f definida por f(x)=A*r^x y coefcor el coeficiente de correlación lineal (de ln(y) con x). Cuanto más cerca esté este coeficiente de 1, mejor será la correlación.
#1 : la matriz de dos columnas que contiene las coordenadas de los puntos (abscisas en la primera columna).
Nuestra nueva construcción macro es parte de su figura.
Para guardarla en un archivo con el sufijo mgc, usamos el ícono de gestionar las construcciones  y elegimos el ítem
y elegimos el ítem
Guardar una construcción de la figura. Lo guardamos como Regresión_Exponencial.mgc.
También es preferible guardar la figura en sí siempre que haya cometido un error al crear la macro construcción.
Ahora probaremos nuestra macro construcción en otra figura.
Creemos una nueva figura con un referencial y con la herramienta  creemos algunos puntos libres como se muestra a continuación para que estén "cerca" de una curva exponencial.
creemos algunos puntos libres como se muestra a continuación para que estén "cerca" de una curva exponencial.
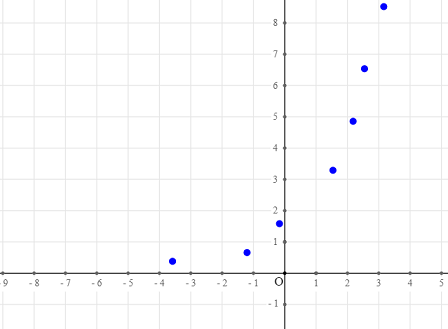
Ahora vamos a pedirle a MathGraph32 que cree una matriz cuyas coordenadas sean las de los puntos creados.
Expandimos la barra de herramientas de cálculos, hacemos clic en el icono  y elija el elemento Matriz de coordenadas.
y elija el elemento Matriz de coordenadas.
Aceptemos el nombre mat como el nombre de la matriz y luego hacemos clic en los puntos creados. Cuando hayamos hecho clic en el último punto, hacemos clic en el botón rojo STOP que está abajo y a la derecha de la ventana.
Si usamos la herramienta  veremos que MathGraph32 ha medido la abscisa y la ordenada de cada punto y luego ha creado una matriz mat formada a partir de estas medidas.
veremos que MathGraph32 ha medido la abscisa y la ordenada de cada punto y luego ha creado una matriz mat formada a partir de estas medidas.
Incorporemos ahora a esta figura nuestra macro construcción de regresión exponencial.
Utilicemos el icono  y elegimos el elemento Incorporar una construcción desde un archivo.
y elegimos el elemento Incorporar una construcción desde un archivo.
Vamos a buscar nuestra construcción a la carpeta donde la guardamos, la seleccionamos y hacemos clic en el botón Abrir. La construcción es ahora parte de la figura.
Nuevamente usemos el ícono  y elijamos el elemento Implementar una construcción de la figura. Elegimos la construcción de regresión exponencial y hacemos clic en el botón Implementar.
y elijamos el elemento Implementar una construcción de la figura. Elegimos la construcción de regresión exponencial y hacemos clic en el botón Implementar.
Se abre un cuadro de diálogo para elegir el único objeto fuente necesario, una matriz. Completamos como se muestra a continuación eligiendo como objeto fuente la matriz mat y validamos.
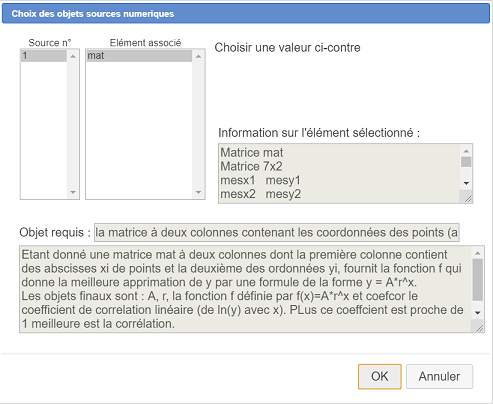
En la barra de herramientas de arriba, usamos el ícono  para ver los objetos numéricos de la figura.
para ver los objetos numéricos de la figura.
En la parte inferior de la lista, veremos los objetos que fueron creados por la construcción, coefcor, A, r y la función f.
Tracemos ahora la curva representativa de f.
En la paleta de colores, activamos el color rojo y luego usamos la herramienta  .
.
Solicitamos que la curva de la función f a trazar sobre R.
Finalmente, mostremos el valor del coeficiente de correlación utilizando la herramienta de visualización de valores  .
.
Hacemos clic en la parte superior izquierda de la figura y completamos el cuadro de diálogo como se muestra a continuación :
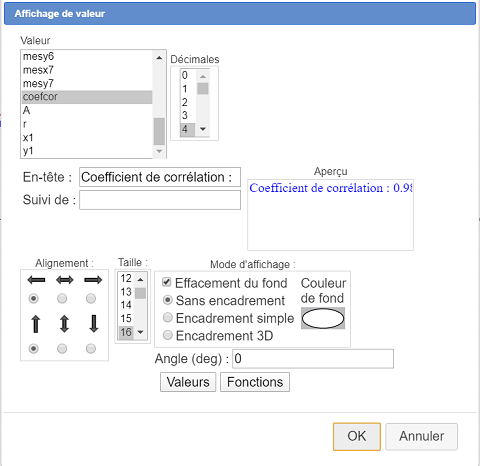
Ahora podemos capturar los puntos de la figura y constatamos que cuanto más lejos estén los puntos de la curva, menos cercano a 1 será el coeficiente de correlación.
A continuación se muestra la figura final :
Podemos descargar estas dos macro construcciones en archivos zip a continuación :